No último post, explicamos o que é o Value at Risk. Nesse post, o foco será no cálculo do Value at Risk na prática. Os três métodos utilizados para calcular o VaR são: (1) o VaR paramétrico, (2) o VaR histórico e (3) simulação de Monte Carlo. Explicaremos melhor o passo a passo do VaR paramétrico e do VaR histórico. A planilha de apoio desse artigo pode ser encontrada neste link.

Base de dados

Para calcular o VaR do seu portfólio, você precisará da base de dados com os retornos das ações que o compõem. Nesse exemplo, utilizaremos os retornos diários do Ibovespa no período de um ano (de 10/04/2019 até 08/04/2020), que foram calculados a partir da série de preços obtida por meio do Google Finance. Com o histórico em mãos, podemos calcular algumas medidas estatísticas da distribuição empírica dos retornos, como a média e o desvio padrão (volatilidade).

VaR Paramétrico

O primeiro passo para calcular o VaR paramétrico é decidir qual a distribuição a ser assumida. O mais comum é assumir que os retornos seguem uma distribuição Normal (Gaussiana), devido a sua simplicidade. A distribuição normal é completamente caracterizada com apenas dois parâmetros: média e desvio padrão. No entanto, outras distribuições podem ser utilizadas, como por exemplo a distribuição t de Student.

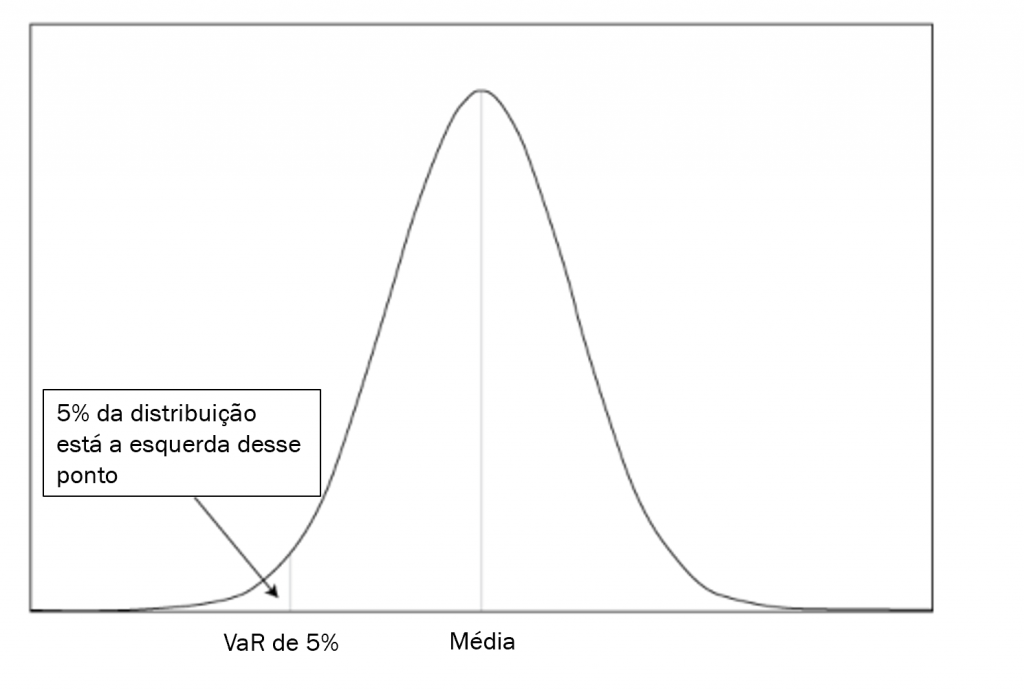
No nosso exemplo utilizaremos a distribuição Normal. Mas quais os parâmetros que devemos utilizar na distribuição? Como estamos utilizando retornos diários, é comum assumir média 0 para facilitar a conta, já que o retorno médio de um dia tende a ser muito próximo de 0. No caso da nossa amostra, notamos que isso é verdade, já que a média é -0,05%. Na aba “VaR Paramétrico” deixamos o cálculo para ambas as escolhas, perceba que o resultado final fica praticamente inalterado. Já em relação ao desvio padrão, o jeito mais simples é assumir o desvio padrão da amostra de retornos históricos. No caso do nosso exemplo, a volatilidade diária é de 2,6%.

Definidos a distribuição e os parâmetros, basta escolher o parâmetro do VaR a ser utilizado. O padrão do mercado costuma ser o VaR de 5%, mas no exemplo fizemos o VaR de 1% (pode ser facilmente alterado para o número mais conveniente na planilha). O parâmetro (n) do VaR significa basicamente que existe uma probabilidade n do retorno diário ser aquele valor ou menos.

No caso da distribuição Normal padrão (de média 0 e desvio padrão 1), se quiséssemos o VaR de 1%, o valor seria -2,33. O de 5%, -1,645 (esses valores podem ser achados com a ajuda da função Inv.Norm para os parâmetros de média 0 e desvio padrão 1). Posto de outra forma, isso equivale a dizer que 5% das observações na distribuição Normal são menores do que -1,645 vezes o desvio padrão e 1% é menor do que -2,33 desvios padrão.

Para transformar a Normal padrão na Normal que melhor representa a distribuição dos nossos retornos, basta multiplicar o valor da Normal padrão pela volatilidade que encontramos acima (2,6%) e somar a média (0% ou -0,05%). Após todo esse processo, chegamos ao VaR paramétrico de 1% de -6% para o Ibovespa. Ou seja, 1% dos dias a queda do Ibovespa será de 6% ou mais, conforme previsto pelo VaR paramétrico.

VaR Histórico

Diferente do VaR paramétrico, o VaR histórico não necessita de nenhuma suposição quanto a distribuição dos retornos. Utiliza-se a própria distribuição histórica, que pode ser representada por um histograma, conforme abaixo.

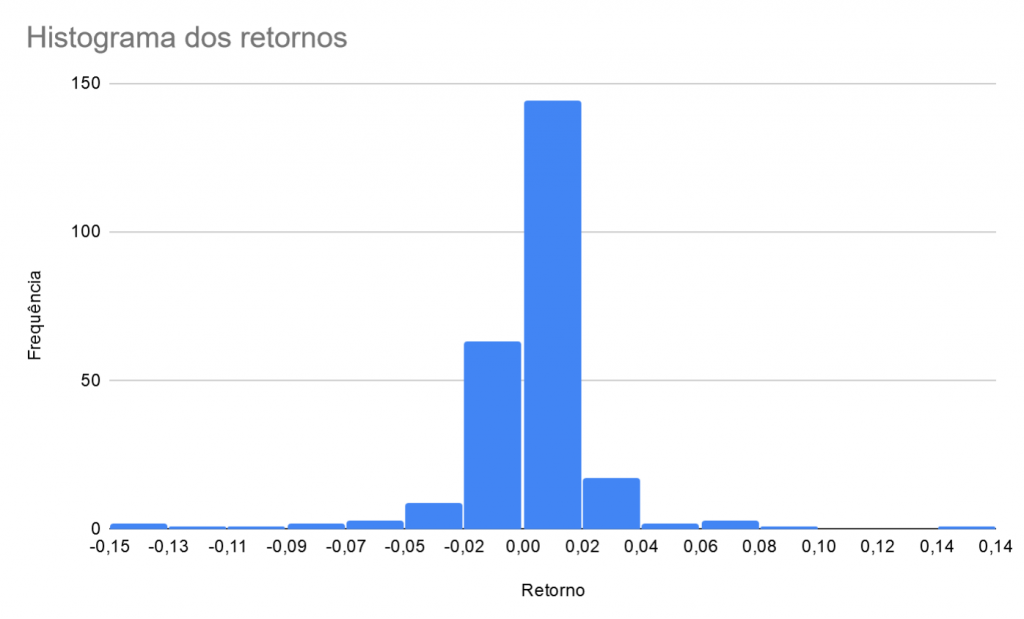
Na nossa amostra temos 249 dias úteis, ou seja, 249 dados de retornos diários. Para calcular o VaR, primeiro deve-se organizar os retornos em ordem crescente. Com a série em mãos, basta decidir o parâmetro do VaR e pegar o retorno correspondente, conforme explicamos abaixo.

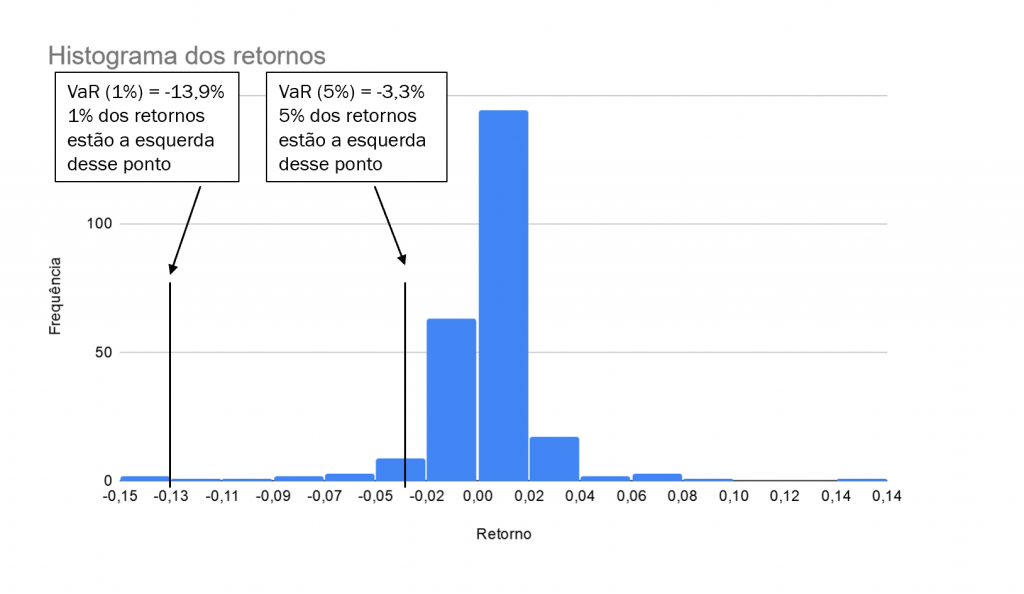
Como temos 249 dados, o VaR de 1% será o segundo menor retorno da amostra (1% de 249 = 2,49 ou 2 arredondando). O VaR de 5%, por sua vez, seria o décimo segundo menor retorno (5% de 249 = 12,45, ou 12 arredondando). Por esse método, o VaR histórico do Ibov de 1% é -13,9%.

Para ficar claro o porquê fazemos isso, basta lembrar da definição do VaR: é a perda mínima esperada x% (nesse caso, 1%) do tempo. Dentro da nossa amostra de 249 dias, 1% dos retornos foram iguais ou inferiores a -13,9%. Ilustramos esse conceito com a imagem abaixo.

Na página de cada um dos fundos (Versa, Fit, Charger e Tracker) você pode ver o VaR histórico e paramétrico diários para os fundos na seção “Parâmetros de Risco”.

E você? Sabe o VaR do seu portfólio? E dos fundos que você investe? Mande suas dúvidas e/ou comentários aqui no site ou através do nosso email contato@versaasset.com.br