A teoria dos jogos é um braço da matemática aplicada que estuda tomadas de decisões entre indivíduos/jogadores quando o resultado final depende das decisões dos outros participantes. Um conceito extremamente importante dentro da teoria dos jogos é o de Equilíbrio de Nash. O Equilíbrio de Nash representa uma combinação de decisões em que nenhum participante tem a ganhar mudando sua própria estratégia.
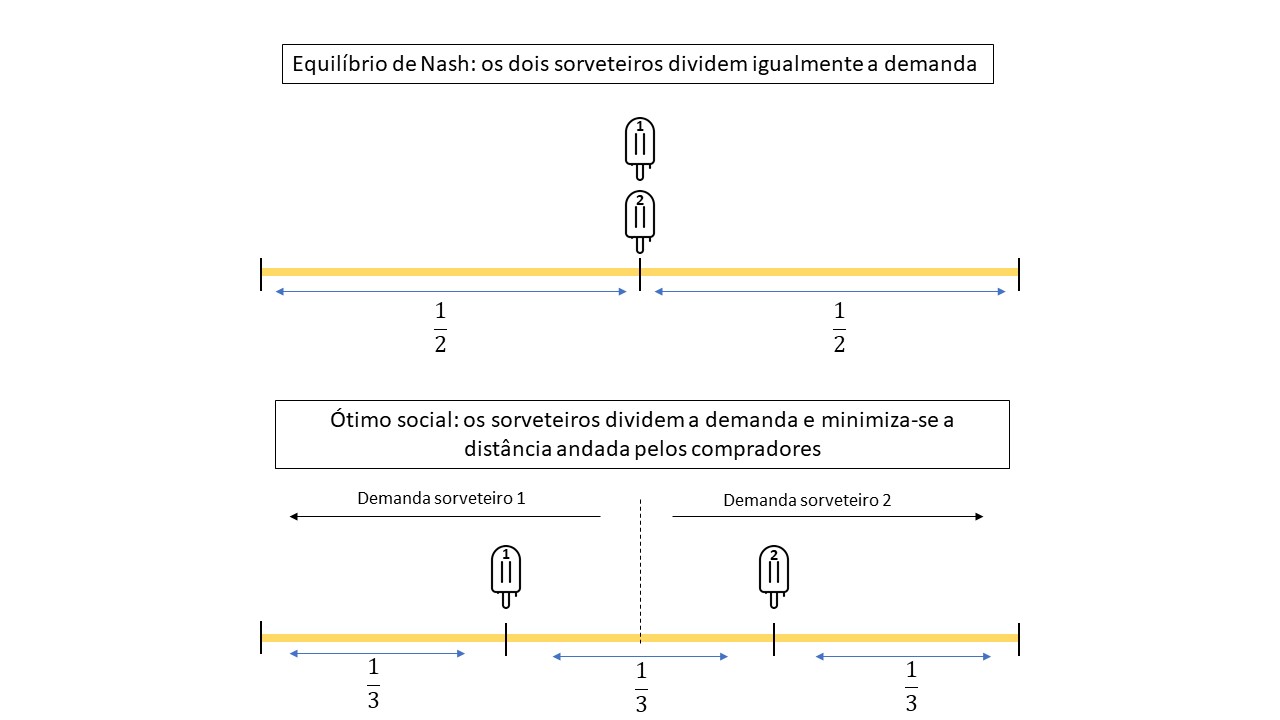
Um jogo simples e bastante estudado é o “Problema dos Sorveteiros”. Imagine uma pequena praia aonde existem 2 sorveteiros que precisam escolher onde colocar seus carrinhos. Para simplificar, vamos assumir que os sorvetes são idênticos, que as pessoas estão distribuídas de maneira igual por toda a praia, e que as pessoas compram o sorvete do sorveteiro que está mais próximo. As vendas do sorveteiro, então, dependerão não apenas de sua própria posição mas também da posição de seu concorrente. Imagine que o sorveteiro numero 1 comece localizado na ponta direita da praia. Nesse caso, a melhor estratégia do sorveteiro 2 será se localizar imediatamente a esquerda do sorveteiro 1, ganhando todos os clientes a esquerda. No momento seguinte, o sorveteiro 1 irá imediatamente para a esquerda do sorveteiro 2, e assim por diante, até que os dois sorveteiros estejam no centro da praia e não haja mais incentivo a se movimentar. Nesse jogo simples, o Equilíbrio de Nash ocorre quando os dois sorveteiros estão exatamente no meio da praia. Vale ressaltar que o Equilíbrio de Nash não tem necessariamente relação com o ponto ótimo social. Nesse caso, apesar do Equilíbrio de Nash ser o ponto ótimo para os sorveteiros, ele não é o ótimo social. A solução ótima social nesse caso seria cada um dos sorveteiros se posicionar em um terço da praia (ou seja, entre uma das pontas e o outro sorveteiro), assim os dois sorveteiros teriam exatamente o mesmo lucro e os consumidores de sorvete teriam que se movimentar menos na média para consumir o sorvete. O ótimo social não é um Equilíbrio de Nash, pois nele há incentivo para os sorveteiros se movimentarem e aumentarem seus lucros.
Apesar de simples e aparentemente pouco útil, o problema dos vendedores de sorvete pode ser usado como arcabouço teórico para assuntos mais complexos como uma eleição, por exemplo. Imagine que a praia seja o espectro político (esquerda-direita), e os sorveteiros sejam candidatos disputando o segundo turno. Nesse caso os consumidores de sorvete são os eleitores. Se, após o primeiro turno um dos candidatos está na extrema direita e o outro na extrema esquerda, a estratégia ótima para os dois candidatos é se aproximar mais do outro até que os dois estejam mais ao centro para angariar o máximo de votos. A lição principal que tiramos dessa simples aplicação é que não importa quão extremos sejam os candidatos que vão ao segundo turno, a tendência para a parte final da corrida eleitoral, se os candidatos forem racionais, deve ser um discurso mais ponderado.
Dá para usar essa teoria para explicar a vitória do Jair Bolsonaro na eleição presidencial de 2018? Se ele adotou ou não um discurso mais moderado no 2o turno, é debatível. Mas acreditamos que a escolha do candidato por não participar de alguns debates pode no mínimo ter reduzido a frequência de suas falas mais polêmicas. Talvez não fosse uma moderação explícita, mas foi na linha do que diz a teoria dos jogos: menos polêmica no final da eleição é a estratégia ótima. Pelo jeito, funcionou.

























